Spherical Parameterization

Spherical parameterization creates a continuous and uniform mapping from the object surface to the surface of a unit sphere, and its result is a bijective mapping between each point 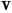on a surface and a pair of spherical coordinates 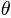and :

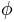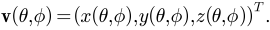
The spherical parameterization method proposed with the original SPHARM paper [Brechb1995] aimed to create an equal area mapping as well as minimize angle distortions by solving a constrained optimization problem, which was implemented in SPHARM-PDM [Styner2006]. This traditional method has been very effective in analyzing small and moderately-sized structures extracted from volumetric images (e.g., MRI, CT). However, it is applicable only to voxel surfaces. CALD [Shen2006] is a newer method that extends the traditional method and can be applied to general triangular meshes. In SPHARM-MAT, an enhanced version of CALD method is available for analyzing triangular meshes (see Exercise 3.1 Surface Meshes (CALD) and Exercise 3.2 Voxel Surfaces (CALD)). In addition, SPHARM-PDM can also be called from SPHARM-MAT for analyzing voxel surfaces (see Exercise 3.3 Voxel Surfaces (PDM)).

Area Distortion Cost

The concept of area distortion cost introduced by [Shen2006] is employed as the performance measure in the following exercises. Let 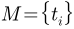be a surface mesh in the object space and let 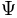be its spherical parameterization, which maps 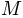to the unit sphere .

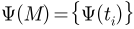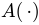is used to denote the relative area of a triangle or a spherical triangle:

• For a triangle, its relative area is defined as its area divided by the total area of the object surface.
• For a spherical triangle, its relative area is defined as its area divided by 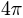, the surface area of the unit sphere.

The area distortion cost (ADC) 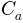with respect to 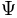is defined as follows:

• For each triangle ,

  

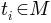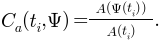
  This measures the local ADC of a single triangle.

• For the whole parametric mesh ,

  

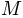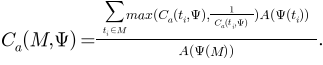
  This measures the overall ADC for the whole mesh. By taking

  

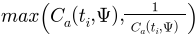
  as the ADC contribution from each triangle, we treat contraction and expansion equally, and so always have .

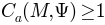Exercise 3.1 Surface Meshes (CALD)

This exercise was tested on a WinXP machine (3GHz CPU, 3.25G RAM) running Matlab 7.7.0 (R2008b). It took a few minutes to finish.

Major Steps

1. CALD Parameterization for Surface Meshes
2. Surface Visualization (ADC_ParaMap, Solid with Mesh)

CALD Parameterization for Surface Meshes

Task

Create spherical parameterization for surface meshes

Input

SpharmMatDir/data/Ex0301/mesh01_obj/*_obj.mat: An input surface needs to be genus zero (i.e., with spherical topology), and can be represented by a triangulation or a quadrilateral mesh.

Output

SpharmMatDir/data/Ex0301/mesh02_smo/initParamCALD/*_ini.mat: Results of initial parameterization

SpharmMatDir/data/Ex0301/mesh02_smo/*_smo.mat: Results of optimized parameterization

Steps

1. Make an output directory SpharmMatDir/data/Ex0301/mesh02_smo
2. Run SPHARM_MAT.m under Matlab
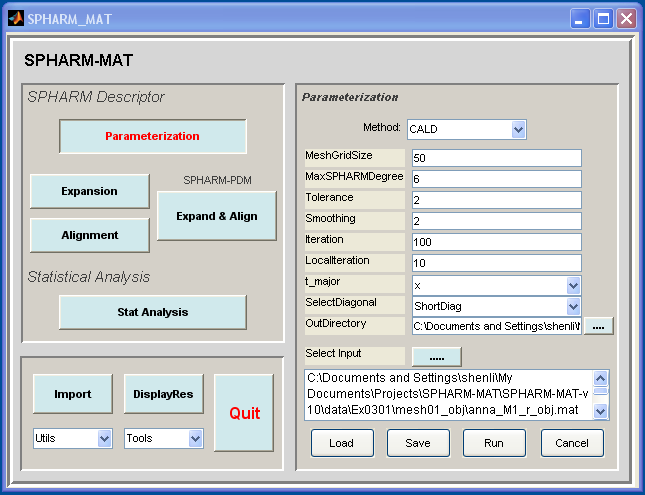
3. Click Parameterization button
4. In the right panel, let Method be CALD
5. In the right panel, let MeshGridSize be 50, MaxSPHARMDegree be 6, Tolerance be 2, Smoothing be 2, Iteration be 100, LocalIteration be 10, t_major be x, SelectDiagonal be ShortDiag.
6. In the right panel, select SpharmMatDir/data/Ex0301/mesh02_smo as OutDirectory
7. In the right panel, click ..... button next to Select Input, and select all the *_obj.mat files under SpharmMatDir/data/Ex0301/mesh01_obj as input files
8. Click OK button (See Screen Capture for CALD Parameterization (Surface Mesh))

Screen Capture for CALD Parameterization (Surface Mesh)

Surface Visualization (ADC_ParaMap, Solid with Mesh)

Task

Visualize surface meshes in both object and parameter spaces

Input

SpharmMatDir/data/Ex0301/mesh02_smo/*_smo.mat or

SpharmMatDir/data/Ex0301/mesh02_smo/initParamCALD/*_ini.mat

Output

SpharmMatDir/data/Ex0301/mesh02_smo/PNG/*.png or

SpharmMatDir/data/Ex0301/mesh02_smo/initParamCALD/PNG/*.png

Steps

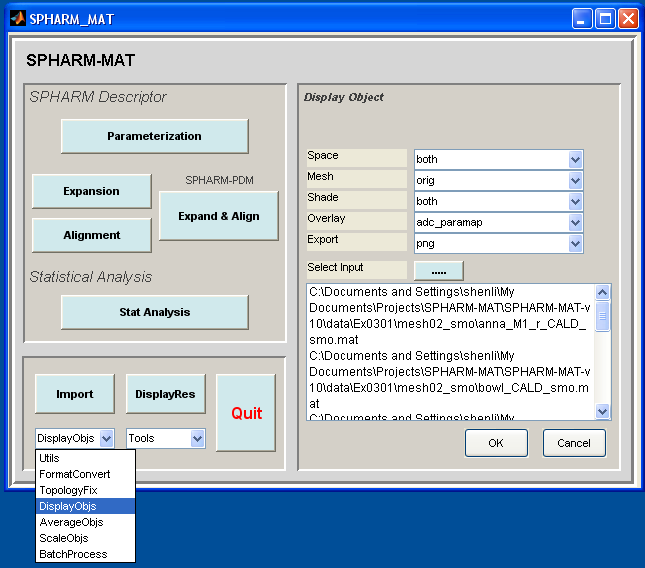
1. Select DisplayObjs under the Utils pop-up menu (bottom-left corner)
2. In the right panel, let Space be both, Mesh be orig, Shade be both, Overlay be adc_paramap, Export be PNG
3. In the right panel, click ..... button next to Select Input, and select either all the SpharmMatDir/data/Ex0301/mesh02_smo/PNG/*.png files or all the SpharmMatDir/data/Ex0301/mesh02_smo/initParamCALD/PNG/*.png as the input files
4. Click OK button (See Screen Capture for Surface Visualization (ADC_ParaMap, Solid with Mesh))

Screen Capture for Surface Visualization (ADC_ParaMap, Solid with Mesh)

Notes

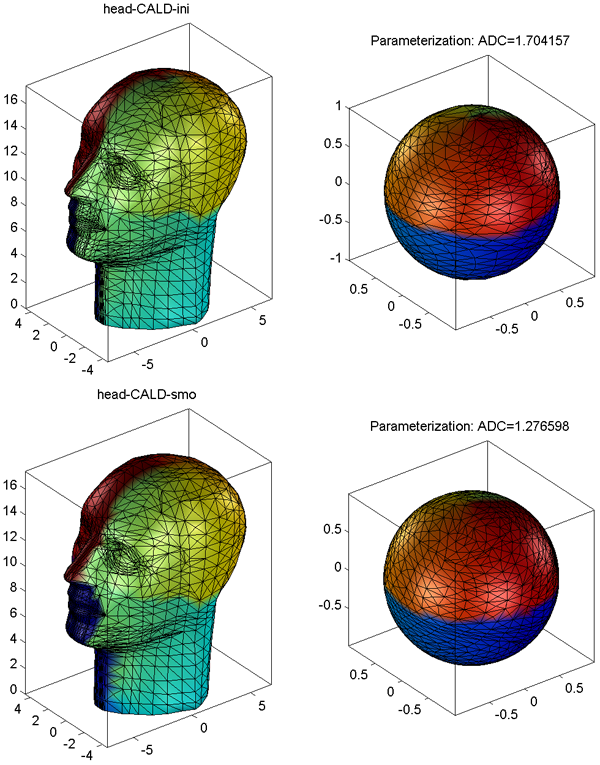
• The visualization results are saved as PNG files under SpharmMatDir/data/Ex0301/mesh02_smo/PNG and SpharmMatDir/data/Ex0301/mesh02_smo/initParamCALD/PNG.
• The results of initial parameterization and optimized parameterization for the head model are shown in Surface Visualization (ADC_ParaMap, Solid with Mesh), where the ADC (area distortion cost) is defined in Area Distortion Cost.

Surface Visualization (ADC_ParaMap, Solid with Mesh)

Relevant Information

Useful Tips

• Parameterization CALD Input and Output
• Parameterization CALD Parameters
• DisplayObjs Space Option
• DisplayObjs Shade Option
• DisplayObjs Overlay Option
• DisplayObjs Export Option
• Data Structure
• File Selection

Exercise 3.2 Voxel Surfaces (CALD)

This exercise was tested on a WinXP machine (3GHz CPU, 3.25G RAM) running Matlab 7.7.0 (R2008b). It took 10-20 minutes to finish.

Major Steps

1. CALD Parameterization for Voxel Surfaces
2. Surface Visualization (ADC_ParaMap, Mesh)

CALD Parameterization for Voxel Surfaces

Task

Create spherical parameterization for voxel surfaces using CALD

Input

SpharmMatDir/data/Ex0302/hip02_fix/*_fix.mat: This folder is a copy of SpharmMatDir/data/Ex0201/hip02_fix/*_fix.mat. The surface of an input binary object needs to be genus zero (i.e., with spherical topology).

Output

SpharmMatDir/data/Ex0302/hip03_smo/initParamCALD/*_ini.mat: Results of initial parameterization

SpharmMatDir/data/Ex0302/hip03_smo/*_smo.mat: Results of optimized parameterization

Steps

1. Make an output directory SpharmMatDir/data/Ex0302/hip03_smo
2. Run SPHARM_MAT.m under Matlab
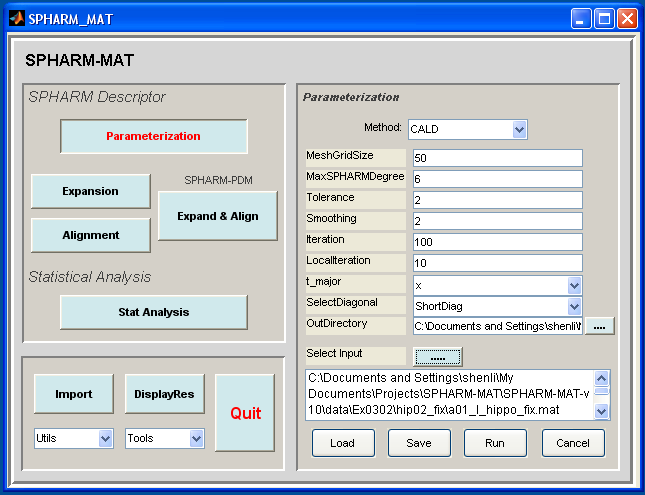
3. Click Parameterization button
4. In the right panel, let Method be CALD
5. In the right panel, let MeshGridSize be 50, MaxSPHARMDegree be 6, Tolerance be 2, Smoothing be 2, Iteration be 100, LocalIteration be 10, t_major be x, SelectDiagonal be ShortDiag.
6. In the right panel, select SpharmMatDir/data/Ex0302/hip03_smo as OutDirectory
7. In the right panel, click ..... button next to Select Input, and select all the *_fix.mat files under SpharmMatDir/data/Ex0302/hip02_fix as input files
8. Click OK button (See Screen Capture for CALD Parameterization (Voxel Surface))

Screen Capture for CALD Parameterization (Voxel Surface)

Surface Visualization (ADC_ParaMap, Mesh)

Task

Visualize surface meshes in both object and parameter spaces

Input

SpharmMatDir/data/Ex0302/hip03_smo/*_smo.mat or

SpharmMatDir/data/Ex0302/hip03_smo/initParamCALD/*_ini.mat

Output

SpharmMatDir/data/Ex0302/hip03_smo/PNG/*.png or

SpharmMatDir/data/Ex0302/hip03_smo/initParamCALD/PNG/*.png

Steps

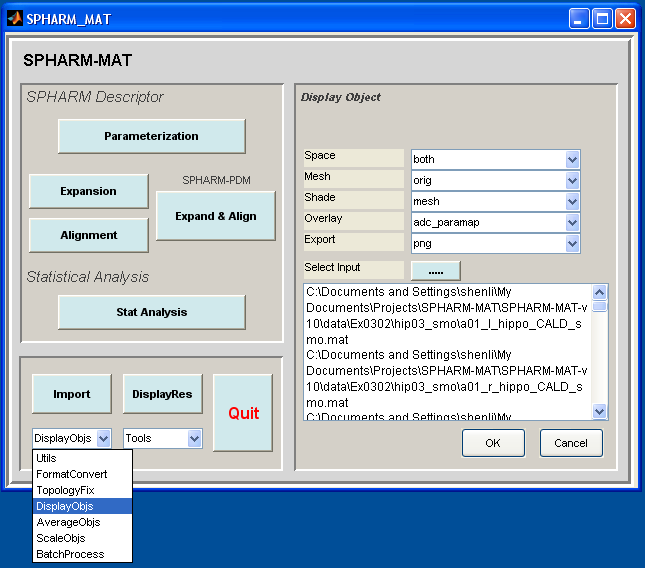
1. Select DisplayObjs under the Utils pop-up menu (bottom-left corner)
2. In the right panel, let Space be both, Mesh be orig, Shade be mesh, Overlay be adc_paramap, Export be PNG
3. In the right panel, click ..... button next to Select Input, and select either all the SpharmMatDir/data/Ex0302/hip03_smo/PNG/*.png files or all the SpharmMatDir/data/Ex0302/hip03_smo/initParamCALD/PNG/*.png as the input files
4. Click OK button (See Screen Capture for Surface Visualization (ADC_ParaMap, Mesh))

Screen Capture for Surface Visualization (ADC_ParaMap, Mesh)

Notes

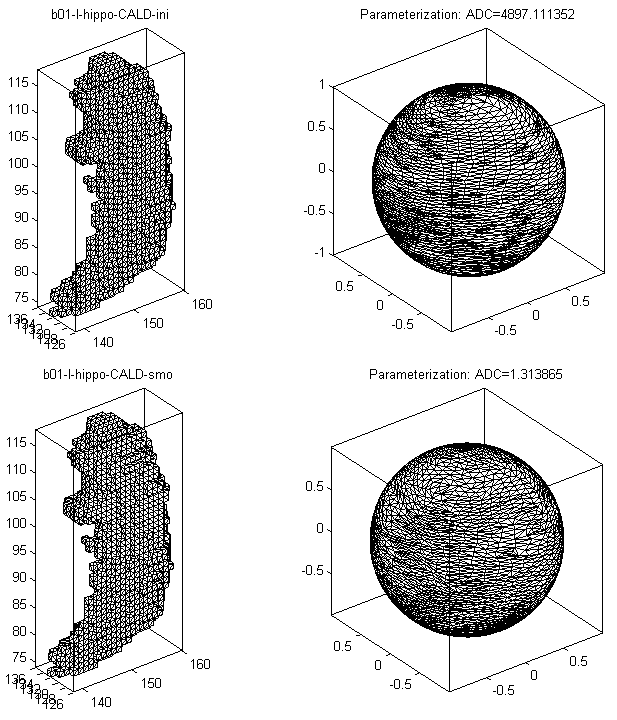
• The visualization results are saved as PNG files under SpharmMatDir/data/Ex0302/hip03_smo/PNG and SpharmMatDir/data/Ex0302/hip03_smo/initParamCALD/PNG.
• The results of initial parameterization and optimized parameterization for a hippocampus are shown in Surface Visualization (ADC_ParaMap, Mesh), where the ADC (area distortion cost) is defined in Area Distortion Cost.

Surface Visualization (ADC_ParaMap, Mesh)

Relevant Information

Useful Tips

• Parameterization CALD Input and Output
• Parameterization CALD Parameters
• DisplayObjs Space Option
• DisplayObjs Shade Option
• DisplayObjs Overlay Option
• DisplayObjs Export Option
• Data Structure
• File Selection

Exercise 3.3 Voxel Surfaces (PDM)

This exercise was tested on a WinXP machine (3GHz CPU, 3.25G RAM) running Matlab 7.7.0 (R2008b) and SPHARM-PDM (WinXP-v1.3). It took 30-40 minutes to parameterize all 40 objects.

Major Steps

1. PDM Parameterization for Voxel Surfaces
2. Format Conversion surf_para_meta2smo
3. Surface Visualization (ADC_ParaMap, Solid with Mesh)

PDM Parameterization for Voxel Surfaces

Task

Create spherical parameterization for voxel surfaces using SPHARM-PDM

Input

SpharmMatDir/data/Ex0303/hip03_gipl_fix/*_fix.gipl: This folder is a copy of SpharmMatDir/data/Ex0202/hip03_gipl_fix/*_fix.gipl. The surface of an input binary object needs to be genus zero (i.e., with spherical topology).

Output

SpharmMatDir/data/Ex0303/hip04_meta/*.meta: Object and parameter meshes are stored in *_surf.meta and *_para.meta respectively.

Steps

1. Make an output directory SpharmMatDir/data/Ex0303/hip04_meta
2. Run SPHARM_MAT.m under Matlab
3. Click Parameterization button
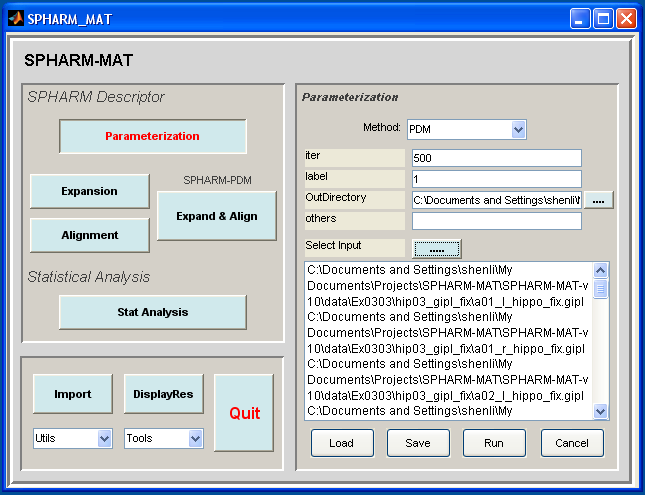
4. In the right panel, let Method be PDM
5. In the right panel, let iter be 500, label be 1, others be empty.
6. In the right panel, select SpharmMatDir/data/Ex0303/hip04_meta as OutDirectory
7. In the right panel, click ..... button next to Select Input, and select all the *_fix.gipl files under SpharmMatDir/data/Ex0303/hip03_gipl_fix as input files
8. Click OK button (See Screen Capture for PDM Parameterization (Voxel Surface))

Screen Capture for PDM Parameterization (Voxel Surface)

Format Conversion surf_para_meta2smo

Task

Convert META surface format generated by SPHARM-PDM to matlab format

Input

SpharmMatDir/data/Ex0303/hip04_meta/*.meta

Output

SpharmMatDir/data/Ex0303/hip05_smo/*_smo.mat

Steps

1. Make an output directory SpharmMatDir/data/Ex0303/hip05_smo/
2. Run SPHARM_MAT.m under Matlab
3. Select FormatConvert under the Utils pop-up menu (bottom-left corner)
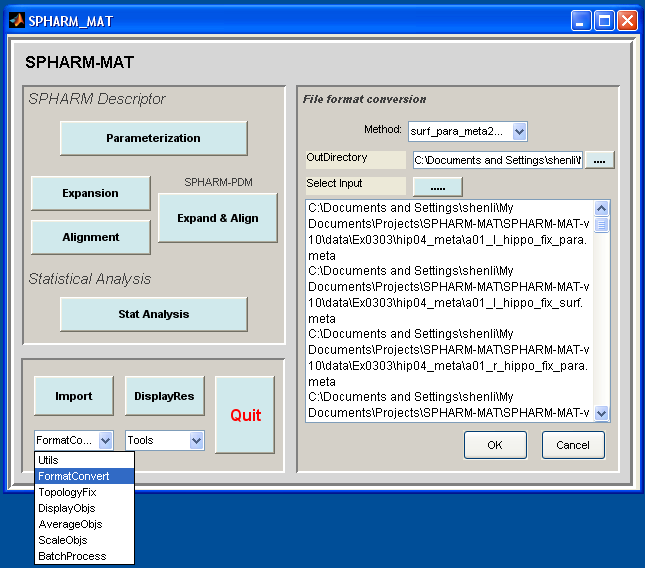
4. In the right panel, let Method be surf_para_meta2smo
5. In the right panel, select SpharmMatDir/data/Ex0303/hip05_smo/ as OutDirectory
6. In the right panel, click ..... button next to Select Input, and select all the *.meta files under SpharmMatDir/data/Ex0303/hip04_meta/ as input files
7. Click OK button (See Screen shot for Format Conversion surf_para_meta2smo.)

Screen shot for Format Conversion surf_para_meta2smo.

Surface Visualization (ADC_ParaMap, Solid with Mesh)

Task

Visualize surface meshes in both object and parameter spaces

Input

SpharmMatDir/data/Ex0303/hip05_smo/*_smo.mat

Output

SpharmMatDir/data/Ex0303/hip05_smo/PNG/*.png

Steps

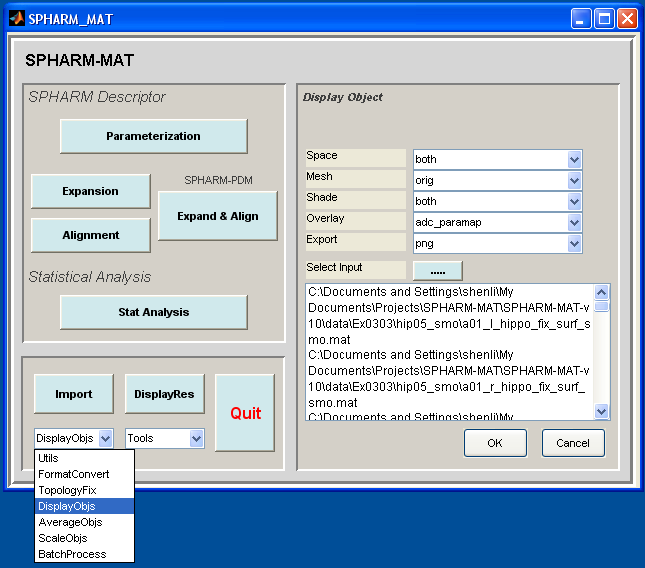
1. Select DisplayObjs under the Utils pop-up menu (bottom-left corner)
2. In the right panel, let Space be both, Mesh be orig, Shade be both, Overlay be adc_paramap, Export be PNG
3. In the right panel, click ..... button next to Select Input, and select all the SpharmMatDir/data/Ex0303/hip05_smo/PNG/*.png files as the input files
4. Click OK button (See Screen Capture for Surface Visualization (ADC_ParaMap, Solid with Mesh))

Screen Capture for Surface Visualization (ADC_ParaMap, Solid with Mesh)

Notes

• The visualization results are saved as PNG files under SpharmMatDir/data/Ex0303/hip05_smo/PNG.
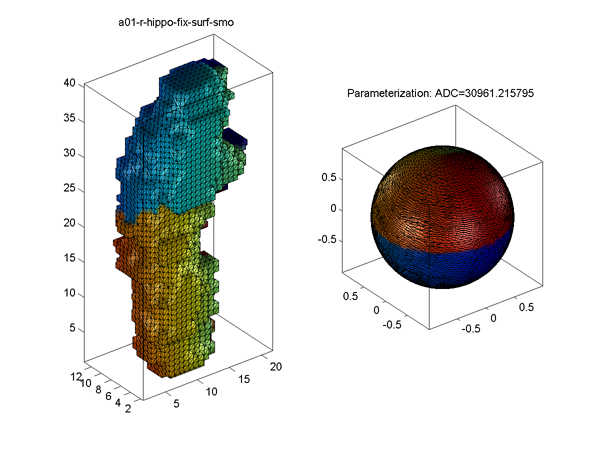
• The parameterization result for a hippocampus is shown in Surface Visualization (ADC_ParaMap, Solid with Mesh), where the ADC (area distortion cost) is defined in Area Distortion Cost.
• To understand why ADC is so high in this example, see ADC Calculation for Voxel Surface and Its Triangulation.

Surface Visualization (ADC_ParaMap, Solid with Mesh)

Relevant Information

Useful Tips

• ADC Calculation for Voxel Surface and Its Triangulation
• Parameterization PDM Input
• Parameterization PDM Parameters
• Format Conversion for Surface Meshes
• DisplayObjs Space Option
• DisplayObjs Shade Option
• DisplayObjs Overlay Option
• DisplayObjs Export Option
• Data Structure
• File Selection